Полный текст - http://osh9.narod.ru/bes/blum.htm
Для начала
ознакомимся с представлениями о массе
микрочастиц видного теоретика, специалиста
по микрочастицам Окуня
Л.Б. [1].
12.
П р и р о д а массы — в о п р о с № 1 с о в р е м е
н н о й ф и з и ки.
За последние десятилетия произошел большой
прогресс в понимании свойств элементарных
частиц. Была построена квантовая
электродинамика—теория взаимодействия
электронов с фотонами, заложены основы
квантовой хромодинамики — теории
взаимодействия кварков с глюонами
и теории электрослабого взаимодействия. Во
всех этих теориях
частицами переносчиками взаимодействий
являются так называемые
векторные бозоны — частицы, имеющие спин,
равный единице: фотон, глюоны, WC и ZC бозоны.
Что касается масс
частиц, то здесь достижения гораздо более
скромные.
На рубеже XIX и XX столетий существовала вера,
что масса может иметь
чисто электромагнитное происхождение, по
крайней мере, для электрона.
Сегодня мы знаем (?), что электромагнитная
доля массы электрона
составляет малую долю его полной массы. Мы
знаем (?), что основной
вклад в массы протонов и нейтронов дают
сильные взаимодействия, обусловленные
глюонами, а не массы кварков, входящих в
состав протонов и нейтронов.
Но мы совершенно
ничего не знаем (!) о том,
чем обусловлены массы шести лептонов (электрона,
нейтрино и еще четырех аналогичных им
частиц) и шести кварков (из которых три
первых существенно легче протона,
четвертый — немного, а пятый в пять раз
тяжелее протона, а шестой
настолько массивен, что его пока не удалось
создать и обнаружить).
Существуют
теоретические догадки, что в создании масс
лептонов и
кварков, а также WC и ZC бозонов решающую роль
играют гипотетические частицы со спином,
равным нулю. Поиски этих частиц — одна из основных
задач физики высоких энергий.
Формула
Е = mс2
появилась
в 1900 г., до создания теории относительности.
Написал ее А. Пуанкаре,
который исходил из того, что плоская
световая волна, несущая энергию
Е,
несет импульс р,
абсолютная величина которого, в
соответствии с теоремой Пойнтинга, равна
Е/с.
Используя
нерелятивистскую формулу Ньютона для
импульса
p = mv
и
учитывая,
что для света p
= mc,
Пуанкаре
[2] пришел к выводу, что
фотон
должен
обладать инертной массой
m = Е/с2.
Позиция академика
Гинзбурга В.Л. является, как всегда,
решительной.
«…
Казалось бы, при знании сути дела речь
идет о вкусах и спорить здесь не о чем.
Однако поступившее в УФН письмо Р.И. Храпко,
преподавателя одного из московских вузов,
свидетельствует о том, что единство
взглядов в вопросе о массе еще не
достигнуто. Полное единомыслие в такого
рода вещах вряд ли достижимо, а где и когда
нужно остановиться в подобного спорах,
заранее не ясно».
А теперь
перейдем к достаточно авторитетным
энциклопедическим данным по вопросу о
массе [3].
«В
принципе ниоткуда не следует, что масса,
создающая поле тяготения, определяет и
инерцию того же тела. Однако опыт показал,
что инертная и гравитационная массы
пропорциональны друг другу (а при обычном
выборе единиц измерения численно равны).
Этот фундаментальный закон природы
называется принципом эквивалентности.
Этот факт был
установлен опытным путем итальянским
ученым Г. Галилеем (принцип
эквивалентности Галилея – авт.) и
может быть сформулирован как принцип
строгой пропорциональности гравитационной,
или тяжелой, массы mT,
определяющей взаимодействие тела с
полем тяготения и входящей в закон
всемирного тяготения Ньютона, и инертной
массы mи
, определяющей сопротивление тела
действующей на него силе и входящей во
второй закон механики Ньютона.
Экспериментально
принцип эквивалентности Галилея
установлен с очень большой точностью – до 10
–12 (в 1971).
Природа массы –
одна из важнейших еще не решенных задач
физики. Принято считать, что масса
элементарной частицы определяется полями,
которые с ней связаны (электромагнитным,
ядерным и др.) (Это
предположение является наиболее вероятным
– автор). Однако
количественная теория массы еще не создана.
Не существует также теории, объясняющей,
почему массы элементарных частиц образуют
дискретный спектр значений, и тем более
позволяющей определить этот спектр.
Тем не менее,
механизм формирования инертной (полевой)
массы электрона и электромагнитной инерции
силовых полей достаточно успешно решается
в рамках Классической электродинамики [4]
, что мы и рассмотрим
чуть ниже.
ОПРЕДЕЛЕНИЕ СОБСТВЕННОЙ ЭНЕРГИИ И ПОЛЕВОЙ МАССЫ ЭЛЕКТРОНА
Масса – физическая
величина, одна из основных характеристик
материи, определяющая инерционные и
гравитационные свойства объектов [3].
Понятие массы было введено в механику И.
Ньютоном в определении импульса (количества
движения) тела – импульс
р пропорционален
скорости свободного движения тела
v: p
= m
v,
где
коэффициент пропорциональности
m
- постоянная в обычной механике
величина, его масса.
Эквивалентное
определение массы получается
из уравнения движения классической
механики Ньютона:
F
= m
a
, где
F
– действующая на
тело сила и
a - ускорение, с которым движется тело.
Определенная таким образом масса
характеризует инерцию тела и называется
инертной массой.
В теории
гравитации Ньютона (в законе всемирного
тяготения) масса тел выступает как источник
поля тяготения (так называемая
гравитационная масса).
О МЕХАНИЗМЕ ФОРМИРОВАНИЯ ЭЛЕКТРОМАГНИТНОЙ (ИНЕРЦИОННОЙ) МАССЫ ЭЛЕКТРОНОВ
Сама по себе идея
решения этой задачи очень проста и всем
хорошо известна. Поскольку электрическое
поле электрона способно производить
механическую работу и обладает энергией, то
это поле должно обладать и определенной
инерцией по аналогии с инерцией
электромагнитных волн и света.
В свою очередь,
энергия электрического поля W
эл
определяется
квадратом напряженности электрического
поля Е.
Таким образом, остается всего лишь
проинтегрировать величину
e
0
Е 2 /2
по всему объему электрического поля,
окружающего электрон.
Такую задачу
пытается решать и Фейнман
[5] и приводит следующий
результат:
W
эл = ò
e
0
Е
2
/2 dV
= e 2 / 8p
e
0
r 0 ,
(1)
где
r
0
-
некоторый эффективный радиус электрона.
Однако здесь у
подавляющего большинства физиков-теоретиков возникают непреодолимые
трудности: до какого, все же, предела вблизи
электрона следует брать интеграл?
Фейнман приходит к
таким неутешительным выводам:
«Все идет хорошо до тех пор, пока мы не
переходим к точечному электрону, … где и
начинаются все наши беды, …
поскольку интеграл по объему
становится расходящимся, а количество
энергии, окружающей точечный электрон,
оказывается бесконечным».
Более сорока лет
потратил Фейнман на борьбу с этими
бесконечностями энергии для электронов,
однако эта проблема так и не нашла
удовлетворительного решения.
Подобная ситуация
с электронами должна была, естественным
образом, навести всех физиков на мысль, что
здесь допускается элементарная логическая
ошибка по поводу точечного электрона.
Более
реалистичную позицию по этому поводу
занимает А.Л. Шаляпин [4,
6-7]:
«принятие электрона точечной частицей
является всего лишь идеализацией и
логической ошибкой, поскольку в природе
вряд ли смогут существовать точечные
объекты, проявляя себя вполне реально и
активно взаимодействуя с окружающими
объектами. Более того, мы даже уже научились
вместе с Фейнманом и со студентами
учитывать неточечность электронов при
нахождении запаздывающих потенциалов
Льенара-Вихерта, а также напряженностей
силовых полей частиц [4-6].
И во всех этих случаях ни о каких
бесконечностях не могло быть и речи».
Кроме всего этого,
следует обратить внимание еще на одну
весьма интересную тонкость.
Из-за того, что
электрон все время совершает "как бы
броуновское" движение, т.е. дрожит под
действием "нулевых" - квазиупругих
колебаний физического вакуума-эфира, его
электрическое поле в среднем не является
центральным.
Поэтому в
реальности он выглядит как светящийся (в
электрическом смысле) шарик с некоторым
эффективным радиусом r
0.
По этой причине электрическое поле
электрона нельзя интегрировать до нуля,
чтобы не возникали разного рода
необоснованные бесконечности в силовых
полях электронов.
Как показано
Фейнманом, в результате прямого вычисления
запаздывающих потенциалов и
напряженностей полей движущегося
электрона [5],
при движении электрона со скоростью
v в вакууме-эфире его
электрическое поле увеличивается на
множитель g
= (1- v
2 / c
2 ) –1/2 .
Силовые поля Е
и B
электрона определяются по обычным правилам
дифференцирования, исходя из силовых
запаздывающих потенциалов, которые были
подробно рассмотрены в работах [4-6].
E
= Ñj
-
¶
A/ ¶
t , B =
rot A.
(2)
Опуская детальные
расчеты, которые были проделаны Фейнманом в
работе [5],
приведем сразу наиболее важные результаты.
Для электрона,
движущегося с постоянной скоростью
v
вдоль оси x,
для скалярного запаздывающего
потенциала получено
j
(x, y, z, t) = g
e /4p
e
0
r ‘ ,
(3)
где
g = (1 – v
2 / c
2) –1/2 ,
x
‘ = g
(x
– v
t), r
‘ =( x
‘2 + y
2 + z
2)
1/2.
Совершенно
аналогичным образом вычисляется и так
называемый векторный потенциал
движущегося электрона в тех же условиях
A
= j
v / c 2.
(4)
Подчеркнем,
что данные потенциалы были получены
совершенно вне зависимости от наличия или
знания уравнений Максвелла.
Выражение
(3) напоминает значение потенциала для
статического случая, т.е. когда электрон
неподвижен, только появился множитель
g
и вместо r
стоит r’.
Преобразования
для x’
и r’
соответствуют хорошо известным
преобразованиям Лоренца. При помощи
преобразований Лоренца динамическую
задачу можно, действительно, полностью
свести к статической задаче, если
одновременно произвести преобразование и
для переменной времени
t
[4-6].
После
дифференцирования силовых потенциалов по
формулам (2) получаются следующие
результаты для проекций напряженности
электрического поля [5]
E
x = g
e (x – v t) /4p
e
0
r ‘ 3/2, E y
= g
ey /4p
e
0
r ‘ 3/2, E z
= g
ez /4p
e
0
r ‘ 3/2.
(5)
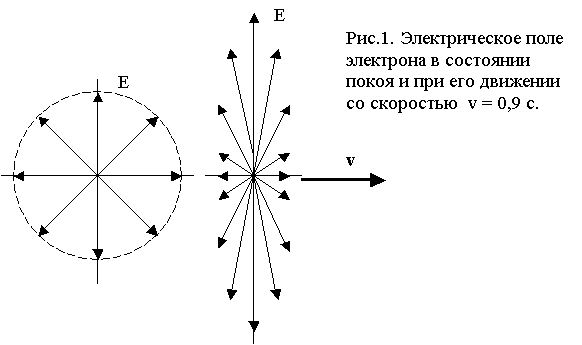
А
теперь вместе с
Фейнманом посмотрим,
как выглядит электрическое поле
движущегося электрона (рис.
1) [5].
Анализируя
компоненты электрического поля, можно
показать, что электрическое поле
движущегося электрона является радиальным,
и силовые линии расходятся от электрона так
же, как и в стационарном случае. Конечно,
вследствие наличия дополнительного
коэффициента g поле не будет тем же самым, что в
стационарном случае. Но здесь мы можем
увидеть нечто очень интересное. Дело
обстоит так, как будто мы записываем закон
Кулона в особой системе координат, «сжатой»
вдоль оси x
множителем g.
Если это представить графически, то силовые
линии впереди и позади движущегося
электрона станут реже, а по бокам сгустятся (рис.1).
Это
означает, что электрическое поле впереди и
сзади электрона ослабевает, но зато по
бокам становится во столько же раз сильнее
в полном соответствии с рассмотренными
уравнениями классической электродинамики.
Но
если электрон движется со скоростью, очень
близкой к скорости света, а это достигается
очень легко в ускорителях, то поле перед
электроном сильно уменьшается, а поле сбоку
электрона чудовищно возрастает. Эту
особенность всегда следует иметь в виду при
рассмотрении взаимодействия очень быстрых
частиц. При этом магнитное взаимодействие
частиц сравняется с электрическим, а
силовые линии вектора В
будут представлять окружности вокруг
линии движения электрона [5].
 |
Остается
подставить E
2 = E
x
2 + E
y
2 + E
z
2 в
выражение для плотности энергии
электрического поля электрона (1) и
проинтегрировать по указанному выше объему.
За счет бокового увеличения электрического
поля движущегося электрона в
g
раз его собственная электрическая
энергия могла бы возрасти в
g2 раз, однако за счет ослабления
поля вдоль оси х
в g
раз результирующая энергия электрона
возрастет ровно в g раз. При этом масса электрона,
которая по своей природе является
электромагнитной, увеличивается во столько
же раз.
Детальные
вычисления показали, что при
интегрировании плотности энергии
электрического поля электрона по объему в
соответствии с формулой (1) мы получаем
увеличение этой энергии, а, следовательно, и
инерции (массы) электрона также в
g
раз. Это с огромной степенью точности
согласуется с экспериментом.
ЗАВИСИМОСТЬ ЭФФЕКТИВНОЙ МАССЫ ЭЛЕКТРОНА ОТ ДВИЖЕНИЯ СОСЕДНИХ ЧАСТИЦ
В классической
электродинамике показывается, что инерция
электрона определяется не только
собственным электрическим полем, но также и
присутствием соседних движущихся
электронов.
Этот случай
является очень примечательным, но иногда
ускользает от внимания исследователей.
В
электрическом поле с напряженностью E на
электрон действует ускоряющая сила
F,
равная
F
=
eE = - e (Ñ j
+ ¶
A /¶
t).
(6)
Оказывается,
что второе слагаемое в скобках
(6) придает электрону
дополнительные инерционные свойства.
Рассмотрим
поведение частицы, движущейся с малой
скоростью вдали от других частиц. В работах [4,
6] показано, что в
свободном пространстве частную
производную в (1) можно заменить полной
производной по времени. Тогда
уравнение (6) можно записать в виде
F
=
d (mv) / d
t = - e Ñj
- e
d A / d
t,
(7)
или
после соответствующей перегруппировки
слагаемых
d/dt
(mv + e
A)
= - e Ñj.
(8)
Следовательно,
частица в электростатическом поле с
потенциалом j
при наличии векторного потенциала А ведет себя таким необычным
образом, как будто ее импульс не
mv,
а некоторый эффективный импульс, равный
pэфф
= m v
+ e A,
(9)
т.е.
зависит также от характера движения
посторонних частиц, формирующих векторный
потенциал А.
Наиболее ярко данный эффект значительного
увеличения инерционности электронов
наблюдается в катушках индуктивности.
Наличие
в (9) дополнительного слагаемого
e
A может привести к появлению
дополнительной инерционности для сложных
частиц (например, ядер, атомов и молекул).
Рассмотрим этот вопрос подробнее.
В качестве примера возьмем один из простейших вариантов движения, а именно, систему, состоящую из двух электрических частиц, например, атом водорода. Поскольку протон намного массивнее электрона, то в первом приближении влиянием электрона на движение протона можно пренебречь.
Пусть
атом водорода движется со скоростью v в
направлении оси ОХ.
Тогда импульс протона с массой
М и импульс
электрона с массой m
соответственно равны
pp
= Mv,
pe
= mv + qAx,
(10)
где
запаздывающий потенциал Ах
создается за счет движения массивного
протона. Здесь мы пренебрегаем орбитальным
движением электрона, поскольку при
усреднении проекция орбитального импульса
на ось ОХ даст
нулевой вклад.
С учетом того, что
А = j v /c 2, (11)
суммарный эффективный импульс атома водорода принимает вид
рэфф
= рр + ре = (М + m + ej
/c 2)v
= (M + m + U/c 2)v,
(12)
где U = e j - потенциальная электростатическая энергия взаимодействия электрона и протона.
Соотношение
(12) можно записать коротко
рэфф
= mэфф v,
где
mэфф = M + m + U/c2.
(13)
Поскольку
в случае атома водорода U < 0, то эффективная масса mэфф становится меньше, чем сумма
масс составляющих частиц. Появился
недостаток (дефект) массы D m,
обусловленный электромагнитным
взаимодействием электрона и протона
D
m = U/c 2.
(14)
При образовании атома водорода избыток энергии DE = - U , а, следовательно, и массы D m был излучен электроном в виде электромагнитных волн, в результате чего полная энергия системы протон + электрон уменьшилась на величину DE по сравнению со свободными частицами, и мы получаем
DE
= c2 D
m.
(15)
В наиболее яркой форме данный эффект проявляется в ядерных реакциях, где благодаря большим энергиям электромагнитного взаимодействия разницу в эффективных массах ядер до и после реакции можно достаточно надежно измерить.
В
работе [8] приводится пример с зеркальными
ядрами изотопов В11 и С11, разница
между которыми состоит лишь в замене
нейтрона на протон в изотопе углерода.
Примечательно, что подобная замена очень
мало отражается на свойствах данных ядер (например,
на схеме уровней возбуждения). Характерной
особенностью данных ядер является то, что
изотоп С11 тяжелее изотопа В11 на
величину электрической энергии протона в
ядре, деленной на с2,
с учетом разницы масс нейтрона и протона, т.е.
в соответствии с формулой (15). Эти данные
говорят о том, что электромагнитные (в
частности кулоновские) силы играют
существенную роль в образовании ядер и в
ядерных реакциях. Учитывая то
обстоятельство, что простые классические
соотношения, рассмотренные в данном
разделе, выполняются с очень высокой
точностью для всех атомов и ядер (при
сравнении эффективных масс элементов),
можно предположить, что электромагнитные
силы являются основными силами,
участвующими в формировании не только
атомов, но также и ядер.
В
заключение нам осталось выяснить, каким
образом ньютоновская масса (инерция) частиц
и силовых полей проникла в классическую
электродинамику, в которой совершенно была
не понята современными физиками.
СВЯЗЬ
ЭНЕРГИИ С МАССОЙ ПО УМОВУ
В одной из неопубликованных
рукописей (1897г. - в
одной из своих лекций в МГУ [9-11])
Умов указывал: "В
умах современных теоретиков эта энергия (т.
е. энергия электромагнитного поля
излучения.- А.
Компанеец [12])
облеклась новыми, непредвиденными
свойствами. Мы привыкли отождествлять
гравитационную массу тела с его инерцией.
Современное учение о лучистой
электромагнитной энергии, по-видимому,
раскалывает такое представление.
Излучаемая энергия является составной
частью массы тела. Излучение света
уменьшает эту массу. Энергия лучей
Максвелла является эквивалентной массе,
как теплота и механическая энергия, и
коэффициент эквивалентности
представляется квадратом скорости света.
Излучение переносит массу от тела,
излучающего к телу абсорбирующему".
В виде формулы это
выглядит так:
dE
= c 2 d m,
где
dE
- излучаемая
телом энергия и d
m
- изменение
массы тела в результате излучения (авт.).
Данное соотношение
между массой и энергией совершенно
естественно и просто следует из волновых
квазиупругих процессов в физическом
вакууме-эфире, а еще более конкретно – из
акустической формулы для
скорости звука в среде с
2 = ¶
p/
¶
r [4]. Здесь
dp
означает малое изменение давления в
упругой волне и однозначно связано с
запасанием в силовом поле упругой энергии
dE,
dr - связано, вполне естественно, с
переносимой в волне массой
dm.
В итоге, из этих волновых закономерностей
мы приходим к совершенно замечательному
следствию о том, что все силовые поля,
базирующиеся на квазиупругих процессах в
физическом вакууме-эфире обладают инерцией,
т.е. массой, и эта масса всегда переносится
вместе с энергией силового поля в
соотношении DE
= c
2 D
m
(авт.).
Таким образом, для
получения соотношения между энергией и
массой (даже ньютоновской) не требуется
изобретать никакой новой физики, тем более,
каких-то туманных принципов и постулатов, а
достаточно просто глубоко вникнуть в
волновые процессы, как это сделал Умов (авт.).
По Умову получается, что все силовые
взаимодействия между объектами природы
происходят через промежуточную
материальную среду (т.е. – физический
вакуум-эфир). И если эта промежуточная среда
является упругой средой, то указанное
Умовым соотношение между энергией и массой
будет выполняться беспрекословно для всех
явлений природы в рамках самой обычной
классической физики [4]
(авт.).
К проблеме о
взаимосвязи и взаимозависимости массы и
энергии Умов возвращался неоднократно. Так,
в своей знаменитой речи "Эволюция
физических наук и ее идейное значение",
произнесенной в 1913 г., он говорил: "Количество
движения или излучается материей, или
принимается ею через электромагнитное, в
частности, световое давление...
Электромагнитное
мировоззрение указывает, что энергия,
связанная с какой-нибудь массой, равна
произведению этой массы на квадрат
скорости света".
Таким образом,
данную зависимость Умов
целиком усматривает в рамках классической
электродинамики, в отличие от туманных
принципов и постулатов последователей Умова
в квазисовременной
абстрактной физике. В дальнейшем было
подтверждено [4],
что данное соотношение достаточно просто
выводится на основе простых волновых (квазиупругих)
процессов в физическом вакууме-эфире, а
также в классической электродинамике (авт.).
Необходимо
отметить, что уравнения движения энергии
получены Умовым для
движения любого вида энергии,
происходящего в любой среде, и таким
образом носят самый общий характер, а не
только для упругой или тепловой энергии в
твердых телах, как это пытаются
интерпретировать очень многие физики и
преподаватели (авт.).
В современной
литературе очень часто все представляется
так, как будто работ Умова
по важным вопросам
фундаментальной физики и не было вовсе, что О.
Хевисайд, Дж.
Пойнтинг, А. Эйнштейн и
др. самостоятельно и независимо пришли к
своим идеям в области классической
электродинамики. На самом деле все наиболее
важные идеи были уже изложены в научных
трудах Умова примерно десятью годами
раньше. Это касается и знаменитого
соотношения между энергией волновых полей
и их инерцией d
E
= c2
d
m.
В работах Умова дословно
приводится пример с переносом части массы
тела dm
посредством излучения с энергией
d
E.
Этот же самый пример, как известно, положил
в основу А. Эйнштейн при выводе формулы E
= m
c
2 .
В Интернете на
сайте: http://www.antidogma.ru/
С.Н Артехи под
заголовком:
ПРОЕКТ
"ВСЕХ НАСТОЯЩИХ ПЕРВЫХ ПОМЯНУТЬ"
представлена
следующая справка:
Так
называемая "эквивалентность массы и
энергии" E = mc²
Формула впервые появилась за
33 года до А. Эйнштейна в
работе
"Die allgemeine Bewegung der Materie als Grundursache aller
Naturerscheinungen", Heinrich Schramm, 1872, Wilhelm Braumüller,
k.k.Hof- und-Universitäts-Buchhändler.
Обсуждалась
в работах Н.А. Умова в 1873 году;
Получена Томсоном в статье "Об
электрическом и магнитном эффекте,
обусловленном движением наэлектризованных
тел", опубликованной в 1881 г. (см. Кудрявцев
П.С. Курс истории физики, М.: Просвещение, 1974);
Получена исходя из теории Максвелла в
работе О. Хевисайда в 1890 году;
В качестве примера
содержится в работе А. Пуанкаре в 1900 году;
Рассмотрена в работе Ф. Газенёрля в 1904 году:
Zur Theorie der Strahlung in bewegten Korpern F. Hasenöhrl,
Ann. Phys.,
Band 15, Seite 344-370, (1904); 16, 589 (1905).
Так
где же здесь приоритет Эйнштейна, который
ввел эту формулу с помощью туманных
постулатов, в отличие от Умова, который
совершенно строго и логически, и
математически задолго до Эйнштейна доказал
это соотношение на основе волновых
классических представлений? При этом
основные идеи в области электромагнетизма
были изложены Умовым в то время, когда
Эйнштейна еще не было на свете (в 1873 году) до
защиты им докторской диссертации в 1874 г.
В дальнейшем было
полностью подтверждено [4],
что соотношение
d
Е =
c
2 d
m
следует из акустики физического
вакуума-эфира, т.е. из самых простых
волновых представлений, как и
предполагалось в работах Умова.
Следует заметить,
что сам Умов незаслуженно скромно оценивал
свои результаты. Он писал, например: "Я
только сказал то, чего другие не договорили,
но что подразумевали для случаев частных. Я
это обобщил и вывел дальнейшие следствия...
Мог бы сказать, что и у Гельмгольца тоже
есть мои зловредные идейки, и я полагаю, что
- и у Максвелла".
Бесспорно, что
обобщения Умова вышли
далеко за рамки "не договоренного" и
"подразумеваемого'" другими физиками [12].
ЛИТЕРАТУРА
1.
Окунь Л.Б. ПОНЯТИЕ МАССЫ (Масса, энергия,
относительность)
Л.
Б. Окунь (Институт
теоретической и экспериментальной физики,
Москва)
УСПЕХИ ФИЗИЧЕСКИХ НАУК. МЕТОДИЧЕСКИЕ ЗАМЕТКИ. Июль 1989 г. Том 158, вып. 3
2.
P o i n c a r e H.//Lorentz Festschrift.—Archieve Neerland, 1900.—V. 5.
P. 252.
3.
Физический
энциклопедический словарь / Ред. Прохоров А.М.
М.: Сов. энциклопедия, 1984. С. 392-393.
773.
4. Шаляпин А.Л., Стукалов В.И. Введение в классическую электродинамику и атомную физику. Второе издание, переработанное и дополненное. Екатеринбург, Изд-во Учебно-метод. Центр УПИ, 2006, 490 с.
5. Фейнман Р., Лэйтон Р., Сэндс М. Фейнмановские лекции по физике. Электродинамика. -М.: Мир, 1977. Вып. 6. С. 265,306.
6. Шаляпин А.Л. О динамике частиц и механизме формирования электромагнитных полей / Урал. политехн. ин-т. Свердловск, 1989. Деп. в ВИНИТИ, 1989. N 118 - В89.
7. Шаляпин А.Л. О природе дефекта масс связанных частиц и релятивистском движении / Урал. политехн. ин-т. Свердловск, 1986. Деп. в ВИНИТИ, 1986, N 8246.
8. Фейнман Р., Лэйтон Р., Сэндс М. Фейнмановские лекции по физике. Электродинамика. – М.: Мир, 1977. Вып. 5. С. 11, 162-168.
9.
Умов Н.А. Курс физики. Лекции, т. 2. Звук. Свет.
Электричество. Магнетизм. М., 1902. См. также
Архив АН СССР, ф. 320, оп. 1, № 83-84.
10.
Умов Н.А. Теория электромагнитного поля.
Архив АН СССР, ф. 320, оп. 1, № 21/3, лл. 1-90.
11.
Умов Н.А. Лекции об электромагнитном поле
(1895). Архив АН СССР, ф. 320, оп. 1, № 100, лл. 1-520.
12.
Компанеец А.И. Борьба Н.А. Умова за
материализм в физике. – Изд-во АН СССР,
Москва, 1954.
За дополнительной информацией можно обратиться на сайты:
http://osh9.narod.ru http://s6767.narod.ru http://s1836.land.ru
http://s1836.narod.ru http://shal-14.boom.ru http://shal-14.narod.ru