КЛАССИЧЕСКИЙ
ПЛАНЕТАРНЫЙ АТОМ В СТАТИСТИЧЕСКОЙ ФИЗИКЕ
Электромагнитная устойчивость атомов
Наиболее наглядно эффективность
последовательного применения законов классической физики в области микромира
можно продемонстрировать на примере объяснения строения атома.
Общепринято считать, что законы классической физики не в состоянии объяснить устойчивость стационарных орбит в атомах. По общим представлениям классической электродинамики электрон, движущийся в атоме по замкнутой круговой или эллиптической орбите, из-за наличия центростремительного ускорения должен излучать энергию в виде электромагнитных волн. Принято также считать, что это излучение должно привести к непрерывной потере энергии и как следствие к падению электрона на ядро.
Действительно, электрон всегда стремится упасть на ядро, если этому ничто не мешает. В тяжелых атомах этому препятствуют нижележащие электронные оболочки. В атоме водорода электрон падает до самого низа к протону и у него остается лишь спиновое движение за счет взаимодействия с "нулевыми" колебаниями физического вакуума-эфира. При этом орбитальный момент электрона уже равен нулю. Это соответствует основному состоянию атома водорода.
Необходимо отметить, что
движение электрона в атоме характеризуется не только полной энергией, но также
механическим моментом и проекцией этого момента на ось симметрии. Если электрон
будет излучать энергию и вследствие этого изменять параметры своей траектории,
то он будет вынужден изменить и характеристики своего механического момента,
который для центральных движений очень тесно связан с полной энергией.
Однако с помощью только одних
поперечных электромагнитных волн электрону не удастся изменить свой механический
момент или его проекцию. Поэтому излучение этих волн без учета изменения
механического момента теоретически невозможно.
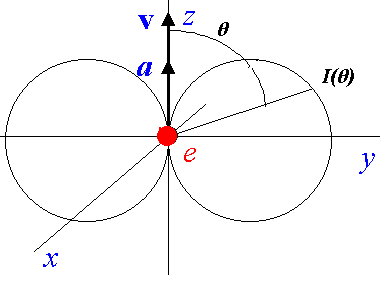
Диаграмма направленности дипольного излучения ускоряющегося электрона представлена
на рис.
1. Она имеет геометрическую форму тела вращения - тора с осью симметрии,
направленной вдоль вектора

Рис.1 Полярная диаграмма распределения интенсивности I дипольного излучения электрона e, движущегося с ускорением а вдоль оси z.
Вполне естественно, что
подобная симметричная относительно радиуса диаграмма направленности не позволит
электрону изменить его механический момент, и, следовательно, в силу закона
сохранения механического момента, существует запрет на изменение полной энергии
электрона.
Простой расчет показывает, что
даже в том случае, если бы диаграмма направленности дипольного излучения была не
симметрична относительно радиуса, то и тогда поперечные электромагнитные волны
не смогли бы обеспечить всё изменение механического момента электрона, поскольку
они слишком легки для этого из-за большой скорости волн с.
Неучет взаимосвязи законов
сохранения энергии и момента количества движения как раз и приводит к
заблуждению, что классическая физика не способна объяснить внутриатомные
явления.
Каким же образом электрон сможет
излучить часть своей энергии с
помощью поперечных электромагнитных волн, находясь на круговой орбите? Для этого
ему необходимо изменить свой механический момент за счет электромагнитного
взаимодействия с другими частицами. То есть излучение и поглощение света атомом
за счет перехода электрона с орбиты на орбиту возможно только при условии
взаимодействия этого электрона с каким-то внешним объектом, могущим обменяться с
электроном механическим моментом.
Для излучения электромагнитных
волн электрону нужен своеобразный катализатор. Можно указать несколько вариантов
такого взаимодействия.
Из опытов известно, что обмен
механическими моментами и энергией
может происходить и между двумя
атомами при их сближении. Такие взаимодействия атомов в газе или плазме носят
название столкновения второго рода. Так, например, в гелий-неоновом лазере за
счет таких столкновений передается энергия возбуждения от атома
Не к атому Ne и обеспечивается инверсия электронной
заселенности рабочего уровня Ne,
без чего невозможна работа лазера.
Можно также предположить, что
обмен моментами между атомами и ионами при их столкновениях существенно влияет
на времена жизни возбужденных состояний атомов и ионов в газоразрядной плазме,
поскольку хорошо известно, что с повышением плотности или температуры плазмы, в
результате чего увеличивается вероятность столкновений, значительно сокращается
время высвечивания атомов и ионов и происходит связанное с этим радиационное
уширение спектральных линий.
Об этом же свидетельствует
устойчивость из-за малой вероятности столкновений сильно возбужденных атомов
водорода с радиусом порядка десятых долей миллиметра - ридберговских атомов,
обнаруженных в последнее время в космическом пространстве
радиоспектроскопическими методами [3-5].
Следует отметить, что очень похожий эффект наблюдается при рождении под действием жесткого электромагнитного гамма-излучения электронно-позитронных пар из физического вакуума (или просто ионизация эфира) вблизи атомных ядер, т.е. при их активном участии.
При этом роль тяжелых ядер
сводится к тому, чтобы принять на себя часть импульса и момента импульса в
процессе вырывания электрона и позитрона посредством электромагнитных волн из
эфира. Без участия же ядер такой процесс не происходит в силу невыполнения
закона сохранения полного импульса и суммарного механического момента системы,
состоящей из электромагнитного поля и вылетающих частиц - электрона и позитрона,
т.е. ядра в этом случае играют роль своеобразного катализатора, способствующего
механизму рождения пар.
Мы видим, что это явление по
своему механизму аналогично процессу поглощения и излучения света атомом. Но
если это первое явление признано физиками, то можно согласиться и с логически
понятным аналогичным объяснением рассматриваемого нами явления излучательных
переходов в атомах.
В качестве примера можно
привести и более знакомое всем явление - внешний фотоэффект, при котором
падающее электромагнитное излучение обеспечивает кинетическую энергию выбитому
из фотокатода электрону, но не может обеспечить фотоэлектрону его импульс. В
этом случае часть импульса (импульс отдачи) принимают на себя атомы твердого
тела, играя роль катализаторов фотоэффекта, т.е. и в данном процессе требуется
выполнение закона сохранения полного импульса системы, участвующей во
взаимодействии.
Инициатором потерь энергии
электрона в атоме могут также служить так называемые «нулевые» колебания
физического вакуума, которые принуждают электрон дрожать и тем самым
обмениваться энергией с окружающей средой.
Таким образом, мы многократно
убеждаемся в необычайной важности выполнения законов сохранения основных
интегралов движения не только в классической макромеханике, но также и в
микромире.
Статистический анализ ансамблей
электронов, находящихся на различных квазистационарных орбитах, позволяет
сделать предположение, что дипольное излучение в такой системе возможно при биениях средней плотности заряда, т.е. на разностных частотах
движения электронов, как это происходит в гетеродинных системах радио- и
телевизионной техники. Отсюда автоматически следует комбинационный принцип
частот Ритца и объяснение спектральных серий атомов. Данное предположение
впервые было высказано Шредингером [6], а также
авторами работы [7].
Как видно из приведенного
рассуждения, орбитальная модель атома просто и естественно объясняется законами
классической физики подобно другим экспериментальным данным, для которых
применимость классических законов не вызывает сомнения.
Обычно якобы
существующую несостоятельность классической физики для объяснения законов
движения электрона в атоме принято демонстрировать на примере рассмотрения
излучения атома, когда движение электрона по окружности заменяется
предполагаемой “эквивалентной” схемой в виде двух электрических диполей,
колеблющихся во взаимно перпендикулярных направлениях с разностью фаз колебаний,
равной p/2
[8,9]. Рассмотрим это утверждение более подробно.
В результате простейшего анализа
характера электромагнитных полей мы придем к выводу, что движущийся по
окружности электрон нельзя заменить эквивалентной схемой, состоящей из двух
электронов, движущихся во взаимно перпендикулярных направлениях или двух
макроскопических диполей, поскольку их электромагнитные поля будут в корне
различаться.
В классической
электродинамике показано, что два скрещенных под углом
90o
электрических макроскопических
диполя при колебаниях с разностью фаз p/2 излучают
поляризованные по кругу поперечные электромагнитные волны в направлении,
перпендикулярном плоскости их колебаний.
Покажем, что исходя из различных
соображений, можно доказать неэквивалентность движущегося по окружности
электрона и двух скрещенных макроскопических диполей.
Прежде всего, в колеблющихся
макроскопических диполях некоторые потенциальные силы периодически совершают
работу над макроскопическими зарядами, при этом происходит периодическое
превращение потенциальной энергии в кинетическую энергию электронов и в энергию
электромагнитного поля движущихся частиц, а затем обратный переход кинетической
энергии частиц и электромагнитного поля в потенциальную энергию системы.
При этом вполне естественно, что
часть электромагнитной энергии поля не возвращается в систему в виде
потенциальной энергии, а уходит на бесконечность в виде поперечных
электромагнитных волн.
Следующим отличием двух
рассматриваемых систем является то обстоятельство, что система колеблющихся
диполей не имеет собственного механического момента, поскольку диполи колеблются
линейно. Поэтому диполи могут излучить всю свою энергию и превратить ее в
поперечные электромагнитные волны, уходящие на бесконечность, без обмена
механическим моментом с окружающими частицами.
В противоположность этому
электрон, обращающийся вокруг ядра по круговой орбите, обладает орбитальным
механическим моментом. Поэтому помимо обмена энергией с электромагнитным полем он должен обмениваться и
механическим моментом. Если у электрона отсутствует канал обмена механическим
моментом с окружающими объектами, то это означает наличие запрета на изменение
полной энергии одноэлектронного атома.
Таким образом, наличие орбитального механического
момента электрона в атоме является главной причиной устойчивости классического
плaнетарного атома. Поэтому
устойчивыми в атоме будут не только круговые электронные орбиты, но также и
эллиптические орбиты, несмотря на различного рода ускорения, которые испытывает
электрон при своем движении.
Более подробно характер движения
электронов в атоме рассматривается в классической статистической физике в работе
[10].
Случайный характер
движения электронов в атомах
Как
известно, в начальной теории Бора рассматривался отдельный изолированный атом
водорода. Однако полностью изолировать атом от внешних воздействий практически
не удается. В реальных условиях электроны атомов всегда подвержены действию
случайных внешних факторов подобно тому, как это имеет место в случае движения
атомов или молекул в газах. Если в газах это проявляется главным образом в
броуновском движении или диффузии частиц, то в случае орбитального движения
электронов в атомах обстановка становится более сложной. Для электронов,
движущихся по атомным орбитам, последствия такого взаимодействия можно разбить
на две группы.
В первую группу следует отнести
такие взаимодействия с внешними факторами, которые приводят к изменению момента
количества движения электрона за счет обмена импульсом или механическим моментом
с другими частицами. Изменение механического момента электрона, как правило,
влечет за собой изменение полной энергии атома и, как следствие, приводит к
излучению или поглощению электромагнитной энергии атомом.
Сюда можно отнести столкновения
второго рода атомов и молекул с изменением внутренней энергии частиц, облучение
атомов быстрыми частицами и электромагнитными волнами с резонансными частотами
поглощения, которые могут привести даже к отрыву электронов от атомов, возможное
взаимодействие орбитальных электронов с нуклонами ядра, играющих роль перевертышей (или катализаторов) для
реализации обмена энергией между орбитальными электронами и электромагнитными
волнами и т.д.
Во вторую группу факторов
внешнего воздействия следует отнести такие более слабые взаимодействия с
окружающей средой, при которых не происходит изменение момента количества
движения орбитальных электронов, например, малые возмущающие воздействия
электромагнитных полей. К таким полям можно отнести: тепловое излучение
окружающих объектов, флуктуирующие переменные ван-дер-ваальсовы поля ближайших
атомов и молекул, вращающиеся стационарные электромагнитные поля всевозможных
электрических и магнитных ротаторов, космические излучения от различных
космических частиц и других космических объектов (в том числе и от космических
ливней), реликтовый фон, электромагнитные колебания физического вакуума - эфира,
т.е. так называемые нулевые колебания, и др.
Вместо перехода
электрона с одной орбиты на другую в атоме, как в первой группе воздействий,
появляется другой не менее существенный процесс - изменение самой формы
стационарной орбиты и ее положения в пространстве, т.е. происходят случайные
вариации орбит.
Траектории в атомах вместо круговых или эллиптических за счет подобного
взаимодействия становятся деформированными и незамкнутыми. Про такую траекторию
обычно говорят, что она размыта или размазана в
пространстве.
На рис.
2 в качестве примера представлен характер движения одного электрона в
атоме водорода при воздействии на него случайных внешних возмущающих полей. За
один период обращения Т траектория электрона вследствие
действия случайных возмущений смещается на некоторую небольшую векторную
величину d r, которая является случайной
как по направлению, так и по модулю (рис. 2,
a).
Если экспериментальное наблюдение за атомом осуществляется в течение промежутка времени D t, за который электрон совершает несколько витков вокруг ядра, то динамические характеристики атома усредняются по пучку траекторий, поскольку из-за наличия случайных возмущений каждая новая траектория электрона не совпадает с предыдущими траекториями (рис. 2, б).
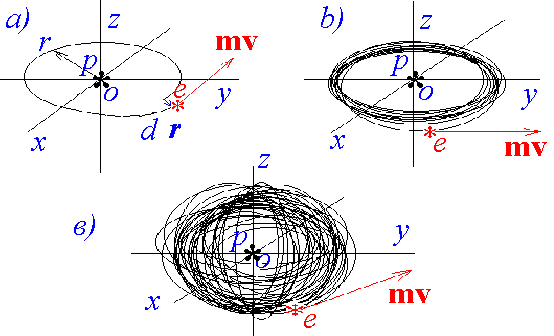
Рис. 2. Траектории электрона в атоме водорода при наблюденииего в течение различных промежутков времени: а) в течение одногопериода обращения Т электрона e вокруг ядра р;б) в течение отрезка времени Dt = 10T; в) в
течение длительного
времени Dt >>T
. |
Подобная ситуация в
корне меняет методику подхода к объяснению и количественному описанию явлений
микромира по сравнению с привычными методами траекторий, применяющихся в
механике Гамильтона. На первый план, как и в броуновском движении, выдвигается
статистический характер взаимодействий. Ибо совокупность случайных смещений
орбит за определенный промежуток времени может быть рассмотрена только методами
статистической физики, фундамент которой был разработан в трудах Максвелла,
Больцмана, Гиббса и их последователей. Статистический подход означает
количественное описание явлений в средних величинах. В этом случае
электромагнитное поле, которое создается электроном в окружающем пространстве,
усредняется по траектории его движения. Кинетическая и потенциальная энергии
электрона также усредняются за время наблюдения. При достаточно малых случайных
возмущениях орбиты полная энергия электрона приближенно может считаться
интегралом движения. Классическими интегралами движения в центральном поле
являются также модуль полного момента количества движения L и его проекция Lz на ось
симметрии атома Z. При этом
можно сказать, что в общем случае L ¹ Lz, поскольку траектория электрона из-за наличия
случайных возмущений или из-за прецессии в магнитных полях не лежит в одной
плоскости, т.е. вектор L совершает либо случайную, либо
стационарную прецессию вокруг оси симметрии Z. Вместо одного атома
статистическими методами может быть рассмотрена сложная система атомов,
состоящая из большого числа одинаковых частиц, находящихся в идентичных
условиях. Большое число частиц в макроскопических телах, т.е. в веществах,
приводит также к появлению статистических закономерностей в поведении таких тел.
Это поведение, точнее их физические свойства, не зависят от конкретных начальных
условий для отдельных частиц, т.е. от точных значений начальных координат и
импульсов всех частиц. Важнейшим проявлением этой независимости является
известный из опыта факт, что система частиц, изолированная от внешних
воздействий, с течением времени приходит в равновесное состояние, свойства
которого определяются только такими общими характеристиками состояния, как число
частиц, их суммарная полная энергия или другие интегралы движения: суммарный
импульс, общий момент количества движения и проекция этого механического момента
на ось симметрии системы [10].
ЛИТЕРАТУРА 1. Фейнман Р., Лэйтон Р., Сэндс М.
Фейнмановские лекции по физике. М.:Мир, 1977. Вып. 3,4. С.41-46. 2. Фейнман Р., Лэйтон Р., Сэндс М.
Фейнмановские лекции по физике. Электродинамика. -М.: Мир,
1977. Вып. 6. С. 144-165. 3. Смирнов Б.М. Высоковозбужденные атомы. М.:
Энергия, 1982. 4. Ридберговские состояния атомов и
молекул / Далгарно А., Дамбург
Р.Я., Колосов В.В. и др. под ред. Стеббингса Р.,
Даннинга Ф. пер. с англ. М.: Мир,
1985. 5. Сильновозбужденные атомы (Обзор).
УФН, 1982. Т.137. В.2. С.
339-360. 6. Джеммер М. Эволюция понятий квантовой механики.
М.: Наука, 1985. 7. Крауфорд Ф. Берклеевский курс физики. Волны.
М.: Наука, 1984. 8. Шпольский Э.В. Атомная физика.
М.: Наука, 1984. Т.1. С.219,241. 9. Ландау Л.Д., Лифшиц Е.М. Теория
поля. М.: Наука, 1980. Т.2. C. 234. 10. Шаляпин А.Л., Стукалов В.И.
Введение в классическую электродинамику и атомную
физику. Второе издание, переработанное и дополненное. Екатеринбург, Изд-во Учебно-метод. Центр УПИ, 2006, 490
с. За дополнительной информацией можно обратиться на сайты: http://s6767.narod.ru http://s1836.land.ru http://s1836.narod.ru http://shal-14.boom.ru http://shal-14.narod.ru Хостинг от uCoz